
‘Looking back at the wake of my ship one day in 1917, I became interested in its beautiful white path. I said to myself, “That path is white because of the different refractions of light by the bubbles of water — H20 (not Hπ0). The bubbles are beautiful little spheres. I wonder how many bubbles I am looking at stretching miles astern?”
‘I began to make calculations of how many bubbles there were per cubic foot of water. I began to find that in calculating the ship’s white wake I was dealing in quintillions to the fourth power times quintillions to the fourth power or some such fantastically absurd number of bubbles. And nature was making those bubbles in sublimely swift ease!
‘Any time one looks carefully at a bubble, one is impressed with the beauty of its structure, its beautiful sphereicity glinting with the colors of the spectrum. It is ephemeral — elegantly conceived, beautifully manufactured and easily broken.
‘Inasmuch as the kind of mathematics I had learned of in school required the use of the XYZ coordinate system and the necessity of placing π in calculating the spheres, I wondered, “to how many decimal places does nature carry out π before she decides that the computation can’t be concluded?” Next I wondered, “to how many aribtrary decimal places does nature carry out the transcendental irrational before she decides to say it’s a bad job and call it off?” If nature uses π she has to do what we call fudging of her design which means improvising, compromisingly. I thought sympathetically of nature’s having to make all those myriad frustrated decisions each time she made a bubble. I didn’t see how she managed to formulate the wake of every ship while managing the rest of the universe if she had to make all those decisions. So I said to myself, “I don’t think nature uses π. I think she has some other mathematical way of coordinating her undertakings.””
— Buckminster Fuller, Your Private Sky, p.457
There’s something here that I like very much (aside from how funny it is to picture the übernerd standing on the back of a ship counting bubbles); that there’s a model of the world that we generally use and which is enough to get by, but isn’t quite right, and that if you disregard that model and consider the qualities of the material itself, you realize that there’s a whole different approach which can be much more fruitful. When Stamen’s working on a project we start by taking a good close look at the data itself and seeing what conclusions emerge, rather than coming up with an external idea which we need to slot the data into, and doing it this way help us avoid having to come up with pi-like approximations which are awkward and inelegant.
It’s this kind of thinking which led to things like Fuller’s Dymaxion Map: why spend all your time trying to fit a round globe onto a single flat sheet, when it makes more sense to break it into triangles and arrange them however you need them? A while ago Mike made what I think is a particularly elegant interactive version of Fuller’s project, which he’s called the faumaxion map (and which you can read more about here):
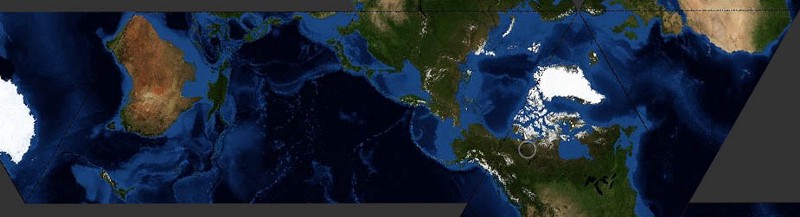
Mike and Tom are going to be speaking about the Faumaxion map, data visualization as a medium, and similarly tasty topics this afternoon during their talk: Live, Vast, and Deep: Web-native Information Visualization at UX Week, Adaptive Path’s fascinating conference on all things related to user experiences on the web.
